✍️ 2023. 10. 20 내용 수정
모수적 방법에 대해 알기전에 모수 Parameter에 대해 알면 좋다.
Parameter라는 단어는 꽤 여러가지 의미를 갖게 되는데 이에 대해선 나중에 언급하도록 하겠다.
모수 Parameter
우리는 모집단 population을 추정하기 위해 표본 sample을 뽑아 조사한다.
선거날 출구조사를 생각해보자.
선거종료 후 개표를 통해 모집단(대한민국 선거인구)이 누굴 뽑았는지 알 수 있지만, 조금 더 빨리 결과를 확인하기 위해 선거하는 사람들 중 몇 명(표본)만 추려서 조사하고 투표가 끝나자마자 출구조사를 공개한다.
만약 출구조사를 통해 A후보가 선출되었다고 발표했다면 이 정보는 통계량(Statistics)이 된다.
그런데, 막상 투표를 까보니 B후보가 선출되었다. 모집단이 누굴 뽑았는가에 대한 정보가 바로 모수(Parameter, 앞으론 모수를 parameter로 표기)다.
parameter는 이처럼 모집단으로부터 나온 결과이며,
위 사례를 통해 parameter가 통계량과 다를 수 있다는 사실을 알 수 있다.
이해를 돕기 위해 parameter를 결과와 연관지었다.
그러나 좀 더 엄격하게 이야기하자면 parameter는 모집단을 대표하는 요약에 해당한다.
무언가를 대표하는 요약은 무엇일까.
예를 들어, 내 얼굴에 대해 묘사해본다고 생각해보자.
정말 많은 표현을 사용할 수 있을 것이다.
그럼에도 딱 떠오르는, 모든 사람들이 공통으로 갖는, 얼굴에 대표적인 특징이 있다.
바로 눈,코,입이다.
눈,코,입을 묘사하면 어느 정도 그 사람의 얼굴이 이렇게 생겼겠거니 떠올릴 수 있다.
만약 내가 당신에게 '나는 눈이 크고, 코가 크고, 입이 작다.'라고 이야기했다면,
당신은 대충 내 얼굴을 어느 정도 상상할 수 있게 된다.
눈, 코, 입은 얼굴을 대표하고 요약하는 훌륭한 특징인 것이다.
모수 Parameter의 예시: 평균 mean, 분산 variance
모집단도 대충 이것만 알면 그 형태를 떠올릴 수 있는 요약이 있다.
가장 흔히 알고 있는 것이 평균(mean)이다.
예를 들어, 100점 만점인 어떤 시험점수의 평균이 30점이다.
대충 이 시험은 굉장히 어려웠을 것이라고 예상할 수 있다.
하지만 평균 하나로는 그림이 덜 그려진다.
우리가 눈에 대한 묘사만 들으면 얼굴의 일부분 밖에 그릴 수 없는 것과 같다.
그래서 보통 parameter로 평균과 함께 분산(variance)을 알려준다.
분산은 평균으로부터 관측치가 얼마나 떨어져있는가를 알려준다.
평균과 분산만 알고 있더라도 대충 모집단의 분포가 어떨지 그려진다.
평균, 분산에 따른 분포의 형태는 아래 그림과 같다.


이제 평균과 분산이 작은지 큰지를 알면(parameter를 알면) 대충 모집단의 그래프가 그려질 것이다.
모집단이 어떻게 생겼는지 어느정도 그릴 수 있다면, 이 형태를 발판 삼아, 모집단을 정확하게 추론할 수 있다.
모수적 방법(Parametric Method)
parametric이라는 단어를 딱 보면 이게 parameter와 관련이 있겠구나 싶은 느낌이 확 올 것이다.
parametric method는 parameter를 가정하고 통계학습을 하겠다는 것이다.
(통계학습 statistical Learning에 대한 설명은 앞선 포스팅을 확인하자.)
[통계 이해땡]예측 vs 추론(통계학습(Statistical Learning)의 목적)
상관관계(Correlation) 야식과 몸무게에 상관관계가 있다고 생각하는가? (난 매우 그렇다고 생각한다.) 그렇다면 어떤 상관관계가 있는지 알고 싶을 수 있다. 예를 들어, 'X번 야식을 먹으면, 몸무게
oooo12.tistory.com
즉, parameter를 가정하고 함수 $f$를 추정하겠다는 의미다.
parameter를 가정하게되면 우리는 대강의 모집단 형태를 가정하는 것과 같다.
이는 함수의 형태를 정해 놓는 것과 같은 말이다.
예를 들어, 모집단의 형태를 직선이라고 가정해보자.
그렇다면 함수의 형태는 당연히 1차 함수, $Y=\beta_0+\beta_1X$ 형태일 것이다.
그렇다면, 함수$f$를 추정하기 위해서 우리가 추정할 것은 단 두가지 밖에 없다.
$\beta_0$와 $\beta_1$ 이 두 개의 수만 알면 된다!
모수적 방법(Parametric Method)의 장점
때문에 parameter를 가정하는 parametric method는 $f$를 추정하기 쉽다는 장점이 있다.
($f$를 추정하는 것을 '적합(fit)한다.'고도 표현한다. parametric method는 적합하기 쉽다.)
또한 parametric method를 사용하면 추론(Inference)하기에도 좋다.
Parametric method는 이미 사람이 정한 가정에 기반하여 논리적인 틀을 갖고 만들어진다.
(논리없이 가정할 수는 없다.) 때문에 태생부터 설명 가능(추론 가능)하다.
모수적 방법(Parametric Method)의 단점
모수적 방법은 비교적 간단한 형태의 함수로 적합한다.
때문에 복잡한 모집단일 경우 모수적 방법으로 예측하면 실제 값과 심각한 차이가 있을 수 있다.
아래 그래프를 보며 이해해보자.
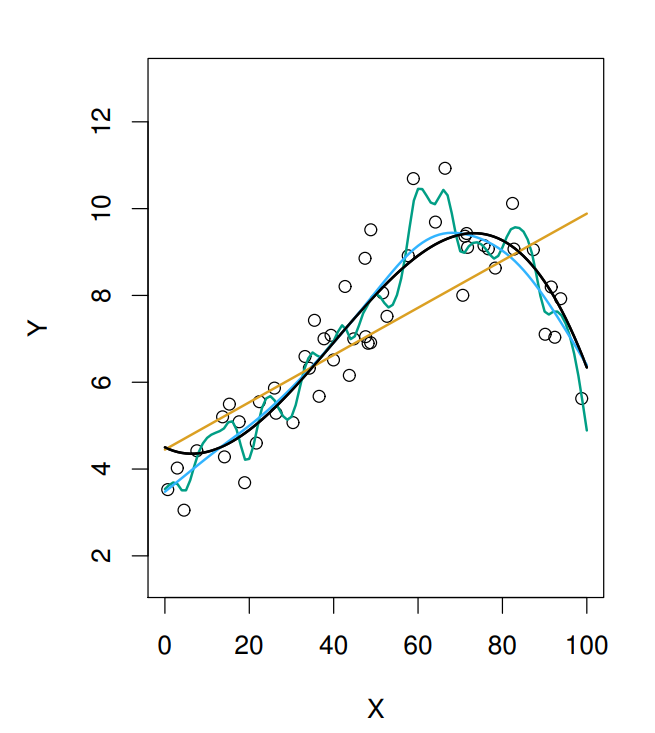
검은색 실선은 모집단, 즉 X에 따른 실제값(Y)이다.
이제 상상해보자.
우리는 검은색 실선을 알지 못한다.
다만, 검은색 실선과 가까운 예측을 하고 싶다.
우리는 좀 더 쉽게 모집단을 추정하기 위해 모수적 방법을 사용했다.
모수적 방법을 사용하기에 우리는 함수의 형태를 가정할 것이다.
함수의 형태를 1차 함수로 가정했다고 생각해보자.
(1차 함수 == $Y=\beta_0+\beta_1X$) 이렇게 나온 결과는 직선인 황색선이다.
예측한 황색선과 실제 모집단인 검은색선을 비교해보자.
황색선과 검은색선 사이에는 꽤 큰 차이가 보인다.
모수적 방법을 사용했을 경우 예측이 부정확할 수 있다는 것이다.
예고: 비모수적 방법(Non-parametric Method)
위 그래프를 잘 보면, 하늘색선이 있다. 이 하늘색 선은 상당히 검은색선과 유사하다. 즉, 굉장히 정확한 예측을 해내고 있다. 이 그래프는 꽤나 복잡하다. 이렇게 복잡한 추정을 해낼 수 있는 방법이 비모수적(Non-parametric Method) 방법이다. 비모수적 방법은 모수적 방법과 달리 예측에 특화되어 있다.
참고
가볍게 시작하는 통계학습: R로 실습하는 An Introduction to Statistical Learning with Applications in R, Gareth James/Daniela Witten/Trevor Hastie/Robert Tibshirani, 마이클 역, 루비페이퍼, 2016
가볍게 시작하는 통계학습 | James, Gareth - 교보문고
가볍게 시작하는 통계학습 |
product.kyobobook.co.kr
2. 기술통계
## 통계량 * 편차 = 관측값 - 평균 = $X_i - \overline{X}$ * 평균 $(\overline{X}) = \frac{\mathsf{\mbox{모든 관측값의 합…
wikidocs.net